Информационный поиск - Адаптивный матричный графический эскиз, вероятность телепортации, вычисление PageRank
0 Wizard 0f Ahhhs [2014-07-17 13:55:00]
Я делаю кое-что в Информационном Извлечении, и у меня есть экзамен, и я абсолютно не знаю. Во-первых, может ли кто-нибудь порекомендовать мне кратчайшее и лучшее описание, возможное для того, что PageRank на самом деле находится в информационном поиске? Может быть, даже хорошее короткое видео или ваше собственное описание. Я знаю, что Google использовал или использовал его.
Я знаю, что здесь есть много вопросов, но я мог бы как можно скорее помочь как можно быстрее за короткий промежуток времени.
Итак, мой первый вопрос (взятый из прошлых статей и составление моих собственных примеров):
Я хочу взять таблицу, такую как:
A B C
A 0 1 0
B 1 0 1
C 0 0 0
И создайте график. Я считаю, что это правильно, но не уверен (я мог бы использовать "да, это правильно" или "нет": 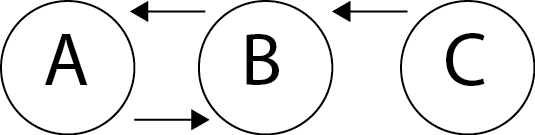
И если мне дали график, например: 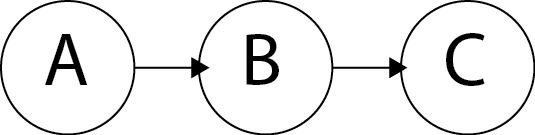
Таблица:
A B C
A 0 1 0
B 0 0 1
C 0 0 0
Это верно? Если нет, могу ли я получить помощь и описать ее где-нибудь? Лекция, которую я читаю, не очень полезна для объяснения, и мой лектор не очень помогает в этом.
Затем мне, вероятно, будет предложено использовать вероятность телепортации в первой таблице. Это отчаянно нуждается в помощи. Если вероятность (специальный символ) = 1/2, означает ли это умножить все, включая 0 в таблице, такую как 0x1/2? также 1x1/2? Это для матрицы вероятностей перехода.
Следующим будет, как я могу вычислить PageRank из приведенной выше матрицы. Использование матричного умножения. В словах или в псевдокоде.
Еще один вопрос, который я хочу знать, повысит ли рейтинг страницы пользователя на twitter, если они последуют за другим пользователем? Я предполагал, что это будет нет, потому что они не следуют за пользователем?
Зависит ли пользовательский pagerank от того, как часто вы находите указанного пользователя, начинаете ли вы с произвольного пользователя и нажимаете на другое случайное лицо и тому подобное, пока не найдете их? Я предполагаю, что это определенно неверно. Потому что они могут не следовать указанному пользователю.
Я знаю, что это много, чтобы спросить. Есть ли у кого-нибудь учебники, которые я могу выполнить для того, что не сложно, и я могу посмотреть и освоить его сегодня?
Спасибо, я очень ценю вашу помощь. Я знаю, что ни один человек не может ответить на них, но может помочь кому-то помочь.
matrix probability pagerank transition information-retrieval
1 ответ
0 Решение Ziggy Eunicien [2014-07-17 20:10:00]
здесь мой удар по ответам на ваши вопросы:
хороший учебный ресурс: http://en.wikipedia.org/wiki/PageRank#Simplified_algorithm (без сомнения, вы его уже видели, но это довольно хороший). Начните там, сначала поймите алгоритм, затем выполните реализацию.
это может быть хороший простой способ реализации? http://pr.efactory.de/e-pagerank-algorithm.shtml
или это: http://www.cs.princeton.edu/~chazelle/courses/BIB/pagerank.htm
Я предполагаю, что вы можете программировать на Python (обычный школьный язык), в этом случае вам может быть интересен пакет для обработки графиков, который имеет вычисления на pagerank: http://networkx.lanl.gov/reference/generated/networkx.algorithms.link_analysis.pagerank_alg.pagerank.html. Если вам нужно написать собственный алгоритм pagerank (очень выполнимый), вы можете использовать его для проверки результатов.
Для вопроса о преобразовании матрицы → графа: ваш профессор должен указать, как направленность кодируется в матрице. Имеет ли 1 в B, C ссылку от B до C или от C до B? Мое предположение было бы от B до C. Если это правда, ваш первый график там неправильный, но второй график в порядке. Направленность очень важна в PageRank.
Я считаю, что вероятность телепортации - вероятность того, что случайный ходок, выполняющий новый шаг, перейдет на случайный узел на графике. Он находится на странице wikipedia под "коэффициентом амортизации". Я не знаю, как это связано с умножением чисел в вашей матрице.
Для вопроса Twitter - да, я думаю, что у вас все в порядке. Связываясь с (или предположительно следуя), второй человек ничего не делает непосредственно для первого игрока, но он, вероятно, увеличивает рейтинг второго лица. На практике могут быть вторичные эффекты, такие как второй человек, замечающий, что первый человек интересен и следит за ними.
второй - последний вопрос - да, одна формулировка алгоритма pagerank является случайным блужданием по ссылкам с частотой встречи узла (страницы), идущего в pagerank.
удачи!